Nous savons qu’une bulle de savon est une sorte de bulle particulière, plus précisément une sphère formé d’un mince film d’eau savonneuse remplis d’air flottant dans l’atmosphère.
Et nous avons également vu précédemment qu'une bulle de savon prend donc la forme qui lui permet d’enfermer un volume d’air donnée dans une surface minimale.
Mais notre problématique est la suivante : Peut-on former des bulles autres que sphériques ?
Grâce à cette partie, nous aurons toutes les réponses à nos questions !
Nous savons qu’une bulle de savon est une sorte de bulle particulière, plus précisément une sphère formé d’un mince film d’eau savonneuse remplis d’air flottant dans l’atmosphère.
Et nous avons également vu précédemment qu'une bulle de savon prend donc la forme qui lui permet d’enfermer un volume d’air donnée dans une surface minimale.
Mais notre problématique est la suivante : Peut-on former des bulles autres que sphériques ?
Grâce à cette partie, nous aurons toutes les réponses à nos questions !
1) Calculs : pourquoi une bulle est-elle ronde au premier abord ?
Nous avons réaliser une série de calculs pour comprendre pourquoi une bulle est ronde.
Nous avons choisis de prendre un volume de 100 cm3 pour chaque solide afin de constater que la plus petite aire est celle de la sphère.
Nous avons réaliser une série de calculs pour comprendre pourquoi une bulle est ronde.
Nous avons choisis de prendre un volume de 100 cm3 pour chaque solide afin de constater que la plus petite aire est celle de la sphère.
La pyramide :
Volume = (Aire de la base x hauteur) /3
Volume = (Aire de la base x hauteur) /3
(hauteur = 12 cm Aire = 25 cm
= (25 x 12)/3
= 100 cm³
Aire = Aire de la base +(( Périmètre de la base x Apothème)/2)
(OD = 12 cm ; DB = 2,5 cm)
(L'apothème est une ligne joignant le sommet de la pyramide au milieu d'un des côtés de la base)
Apothème : BO² = OD² + DB²
Aire totale = 25 + (20 x 12,26)/2
=147,6 cm²
Cube :
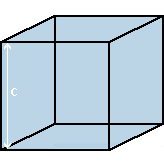 Volume = c³
=³√100 (racine cubique de 100)
≈ 4,642 cm³
Volume = c³
=³√100 (racine cubique de 100)
≈ 4,642 cm³
Aire = 6 x c²
= 6 x (4,642)²
= 129,3 cm²
Sphère :
On calcul r pour pouvoir ensuite
calculer l'aire :
π x r³ = (300/4)
r³ = 300/4)/ π
r³ = (300/4) x (1/π)
r³ = (300/4π) ≈ 23,87 cm³
≈ 2,88 cm
(Le logiciel Géo Gébra nous a également confirmé ce résultat)
Aire = 4 π r²
= 4 x π x 2,88²
= 104,23 cm²
Après ces calculs, on en conclue le résultat suivant :
147,6 cm² > 129,7 cm² > 104,23 cm²
Aire pyramide > Aire cube > Aire sphère
Volume = c³
=³√100 (racine cubique de 100)
≈ 4,642 cm³
Aire = 6 x c²
= 6 x (4,642)²
= 129,3 cm²
Sphère :
On calcul r pour pouvoir ensuite
calculer l'aire :
π x r³ = (300/4)
r³ = 300/4)/ π
r³ = (300/4) x (1/π)
r³ = (300/4) x (1/π)
r³ = (300/4π) ≈ 23,87 cm³
≈ 2,88 cm
≈ 2,88 cm
Aire = 4 π r²
= 4 x π x 2,88²
= 104,23 cm²
147,6 cm² > 129,7 cm² > 104,23 cm²
L'aire de la sphère est donc la plus petite.
Or on sait qu'une bulle tend à prendre la surface minimale. Une bulle est donc ronde car c'est le solide qui prend une surface minimale.
2) Nos expériences sur les bulles de savon
Après avoir compris pourquoi une bulle était ronde, nous nous sommes quand même demandé s'il était tout de même possible de créer des bulles d'une autre forme.
Expérience
Nous avons fait une expérience en salle de TP. Nous avons utilisé la recettede la vidéo « Peut-on faire des bulles carrées ? » de
On n’est pas que des cobayes.
Les ingrédients dont on avait besoin sont :
-12 pailles assez fines
-fil de fer
-un saladier haut
-un verre doseur
-une cuillère
-60 cL d’eau
-20 cL de liquide vaisselle
-50 cL de glycérine
-emporte pièce
-pic à brochette
-scotch
-une paire de ciseaux
-une règle
(-une caméra)

Tout d’abord, nous avons scotché les emportes pièces aux pics à brochette, puis nous les avons trempés dans le mélange eau liquide vaisselle et glycérine que nous avions auparavant mis dans le saladier haut.
On n’est pas que des cobayes.











